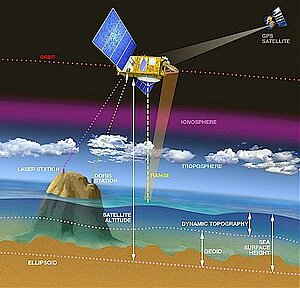
How altimetry works
Altimetry principle
Altimeters emit signals to Earth, and receive the echo from the sea surface, after its reflection. The sea height is represented by the distance satellite - surface and the satellite's position relative to an arbitrary reference surface (the reference ellipsoid).
Some location systems like Doris enable to determine the satellite's position at a high accuracy . We have also to take into account the disturbance suffered by the wave radar. The measurement of these disturbances (by others instruments, or by using multiple frequencies), or their estimation with models, can correct the altimetry measurement. (Credits Cnes).
From radar altimeter to altimeter range (satellite-to-ocean range R)
Radar altimeters on board the satellite permanently transmit signals at high frequency (over 1700 pulses per second) to Earth, and receive the echo from the sea surface. This is analysed to derive a precise measurement of the round-trip time between the satellite and the sea surface. The time measurement, scaled by the speed of light (at which electromagnetic waves travel), yields a range measurement. By averaging the estimates over a second, this produces a very accurate measurement of the satellite-to-ocean range.
However, as electromagnetic waves travel through the atmosphere, they can be decelerated by water vapour or by ionisation. Once these phenomena are corrected for, the final range R is estimated within 2 cm.
The ultimate aim is to measure sea level relative to a terrestrial reference frame. This requires independent measurements of the satellite orbital trajectory, i.e. exact latitude, longitude and altitude coordinates.
Satellite orbit and tracking (S)
The critical orbital parameters for satellite altimeter missions are altitude, inclination and period. Take the Topex/Poseidon satellite. It flies at an altitude of 1330km, on an orbit inclined at 66° to Earth's equator; this is why it can "see" only up to 66° North and South. The satellite on its so-called "repeat orbit" passes over the same ground position every ten days, uniformly sampling the Earth's surface.
The satellite can be accurately tracked in a number of ways. The Doris system on board Topex/Poseidon uses a network of 50 ground beacons, worldwide, transmitting to the satellite. It was developed by Cnes. Doris uses the Doppler shift on the beacon signals to accurately determine the velocity of the satellite on its orbit, and dynamic orbitography models to deduce the satellite trajectory relative to Earth.
Reference ellipsoid
This position is determined relative to an arbitrary reference surface, an ellipsoid. This reference ellipsoid is a raw approximation of Earth's surface, a sphere flattened at the poles. The satellite altitude above the refrence ellipsoid, distance S, is available to within 3 cm.
Sea surface HEIGHT (SSH)
The sea surface HEIGHT (SSH), is the range at a given instant from the sea surface to a reference ellipsoid. Since the sea depth is not known accurately everywhere, this reference provides accurate, homogeneous measurements.
The sea level is simply the difference between the satellite HEIGHT and the altimetric range:
The SSH value takes account of such effects as:
- The sea surface HEIGHT which would exist without any disturbances (wind, currents, tides, etc.). This surface, called the geoid, is due to gravity variations around the world, which are in turn due to major mass and density differences on the seafloor. For example, a denser rock zone on the seafloor would deform sea level by tens of metres, and be visible as a hill on the geoid.
- The ocean circulation, or dynamic topography. The ocean circulation, which comprises a permanent stationary component (permanent circulation linked to Earth's rotation, permanent winds, etc.) and a highly variable component (due to wind, seasonal variations, etc.). The mean effect is on the order of one metre.
To derive the dynamic topography, D, the easiest way would be to subtract the geoid HEIGHT, G, from SSH. In practice, the geoid is not yet known accurately enough, and mean sea level is subtracted instead. This yields the variable part of the ocean signal.