Altimeter drift from tide gauges
Gary T. Mitchum (University of South Florida, USA)
The basic ideas behind using tide gauges as benchmarks for detecting low frequency drift in altimetric sea surface heights are described.
Recent experience gained from analysis of the TOPEX data is briefly reviewed, and the results from that analysis are used to plan a more effective tide gauge set for future use. Finally, some (possibly speculative) projections of the accuracy that might be achievable are presented.
Sea level data measured at tide gauges have been widely used in the past for the purpose of evaluating and validating sea surface heights measured from satellite altimeters, and such intercomparisons with the TOPEX/POSEIDON data (e.g., Mitchum 1994, Cheney et al. 1994) have shown that the two systems agree quite well. Comparisons with tide gauge sea levels are particularly useful because these data in principle measure exactly the same physical variable as the altimeter measures, and also because the in situ data allow an evaluation of the total altimetric system, including environmental corrections as well as instrumental errors, for example.
One consequence of the fact that the altimetric and tide gauge data agree well is that it is reasonable to assume that both systems are measuring the same oceanographic signals.
The variance of the differences between the two data types at any particular tide gauge is typically smaller than the variances of either dataset alone, which is difficult to account for without assuming that both are measuring the same ocean signals. This cancellation of a large part of the ocean signal in the altim-eter minus tide gauge differences allows for a more careful examination of the errors in the measurements.
The type of error that will be discussed here is the possibility of a slow drift in the altimetric heights. Any instrument or measurement system can drift, and requires calibration, or at least monitoring, against an independent set of measurements. Ideally, these independent measurements should come from a simpler, more direct, method. For example, it is generally assumed that tide gauges are subject to slow drifts from a variety of causes. This possibility is constant-ly checked by comparison of the tide gauge sea levels to a set of temporally sparse, but very direct, readings on tide staffs located alongside the gauges. Although the tide staff readings are noisy, and are taken only several times per week, over time these data can be used to monitor the stability of the nearly continuously sampled tide gauge sea levels.
The altimeter and tide gauge systems can be viewed as analogous to the tide gauge and tide staff systems. As compared to an altimeter, a tide gauge is a much simpler and more direct system. And just as the tide staff measurements are temporally sparse as compared to the tide gauge records, the tide gauges are spatially sparse as compared to the altimetric data. But this presents no significant problem for monitoring slow temporal drifts in the altimetric heights.
An early application of these ideas was given by Wyrtki and Mitchum (1990), using data from the Geosat altimeter. These ideas were applied to data from the TOPEX altimeter in a simple fash-ion early in the mission (Mitchum, 1994), and recently a much more careful analysis has been completed. A detailed description of this work has been submitted for publication, and readers interested in it should contact the author.
For the purposes of this article only a brief review of that work will be given.
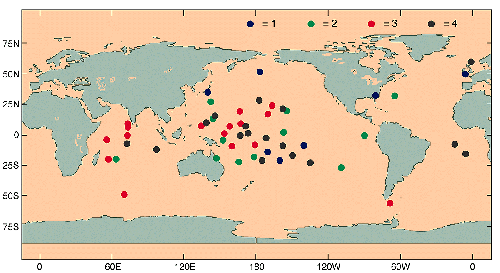
Basically, differences of tide gauge sea levels and nearby altimetric sea surface heights from TOPEX were examined at a large number of sites, and 149 time series of differences from 53 tide gauge stations (Figure 1) were selected for the final analysis. More than one time series per station is possible because the two nearest ascending and two nearest descending altimeter passes were all used independently, although correlations between these time series were accounted for in the analysis. A variety of quality control checks were done on the difference series, and these are described in the paper available from the author.
After selecting these 149 time series, a weighted average was formed of the differences observed during each TOPEX 10-day cycle. The resulting time series of the average TOPEX minus tide gauges value was then interpreted as measuring low frequen-cy TOPEX drift. The weights for the averaging were chosen in order to minimize the variance of the cycle by cycle averages, taking into account the variances of the 149 individual difference series and the correlations between them. Note also that this procedure also results in estimates of the variance of each cycle average.
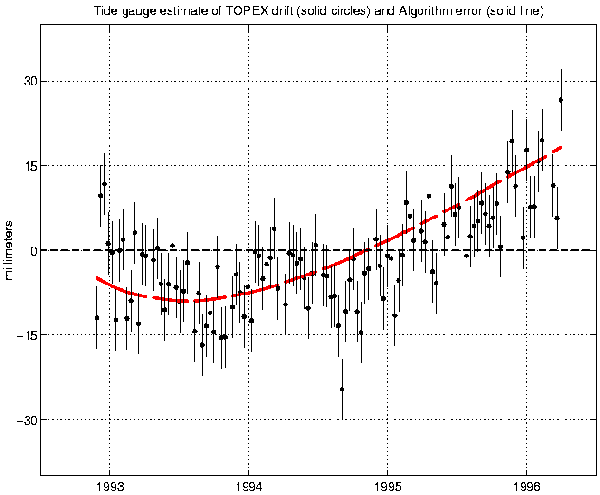
At the time that the above calculation was done, it was not yet known that there was an algorithm error in the TOPEX software that resulted in a low frequency drift in the TOPEX time series. Thus, this error provided an ideal test case for the tide gauge estimate of the TOPEX drift.
That is, there was an unknown drift in the data, which the tide gauges provided a time series for, and then the exact drift was determined independently, giving a way to evaluate the success of the tide gauge method in determining the drift. The tide gauge estimates, along with the now known algorithm error, are shown in Figure 2. Note that the internal error estimates are of order 6 mm, as compared to a 5 mm standard deviation between the tide gauge estimates and the "known" error. It is encouraging that the internal error estimates appear to be rather reliable as well.
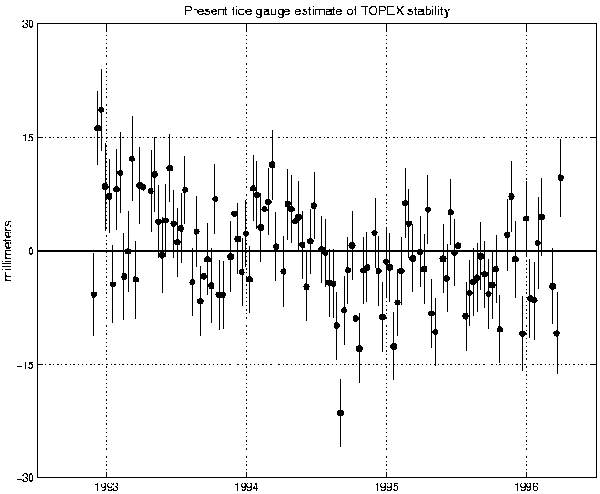
Given this validation of the approach, the corrected TOPEX data were used and the entire analysis was repeated (Figure 3). It is apparent that the altim-eter is now stable to approximately 2 mm/yr, which far exceeds the standards set for the mission. It is also true, however, that the remaining drift, which is of order 2 mm/yr, is too large to be accounted for by the random errors in the tide gauge calculation. Although this level of drift is unlikely to affect the majority of users of the altimetric data, it is very significant to the most demanding applications of the data, such as the determination of low frequency changes in the volume of the global ocean (e.g., Rapp et al. 1994, Nerem 1995, Minster et al. 1995). Consequently we would like to know more about the source of this trend.
Again, the order 2 mm/yr trend cannot be accounted for by the random errors of the analysis. There are at least two sources of systematic error, however, that have to be considered.
First, there is the possibility that the trend results from vertical motion of the land where the tide gauges are located. In my earlier work this possibility was considered in some detail, and I concluded that there was a possible systematic error of about 1 mm/yr. But this error estimate is rather rough. A solution to this problem may be forthcoming, however, with the development of plans to monitor tide gauge vertical motions using GPS receivers (e.g., Carter 1994, Ashkenazi et al. 1993). A plan is presently being formulated to optimize such a network of gauges for the purpose of calibrating altimeters, and my preliminary calculations sug-gest that as few as 10-20 gauges should be able to constrain this sys-tematic error to better than 1 mm/yr. Of course, having fewer than 149 series will inflate the random error, but since this contribution is at present significantly smaller than the possible systematic error, the overall error should decrease.
There is a second type of systematic error that is also being actively investigated at present. In the tide gauge analyses done to date it has been assumed that the altimeter drift is spatially uniform. This seems quite reasonable if one is thinking of an instrumental drift, but is not so clearly acceptable if an environmental correction is suspect. For example, suppose that the sensitivity of the water vapor radiometer was drifting slowly with time. In this case the sea surface height error might be proportional to the total water vapor, and hence be larger in the tropics than at higher latitudes. It is possible to make other examples, but the water vapor one is chosen because there are some indications that this might be a valid interpretation of the observed drift, although a full discussion of this is beyond the scope of this report.
For present purposes it is only necessary to note that it is possible that the drift might be spatially, and particularly meridionally, varying.
This is problematic because the distribution of tide gauges (Figure 1) is heavily biased towards the tropics. This is mainly because the assumption that the error is spatially uniform led to weighting gauges primarily on the basis of small differences with the altimeter, which occurs mostly at island stations in general, and at tropical islands in particular. Simulations are presently being done that relax this condition and search for stations that are better distributed meridionally, yet still constrain the error of the drift time series fairly well. These simulations would be more realistic, however, if the source of the drift, and hence the spatial shape of the expected drift, could be independently determined.
So what are the prospects for the future? First, it should be noted that, while the above discussion has focused on TOPEX sea surface heights, there is nothing in the meth-odology that limits its generality. These methods can be applied to any altimeter. Second, with a careful selection of gauges and the installation of GPS receivers, it is likely that a network of order 20 gauges could monitor the stability of altimeter heights to better than 1 mm/yr over a typical 3-5 year mission. In addition to helping to insure the quality of the altimetric data for the general user, this level of calibration will eventually enable unprecedented studies of the low frequency volume changes of the global ocean, and will also allow confident interpretation of small amplitude decadal fluctuations that might otherwise be suspect.
References
- Ashkenazi, V., R. Bingley, G. Whitemore, and T. Baker, 1993: Monitoring changes in mean sea level to millimeters using GPS. Geophys. Res. Lttrs., 20, 1951-1954.
- Carter, W. (ed.), 1994: Report of the Surrey Workshop of the IAPSO Tide Gauge Bench Mark Fixing Committee. Wormley, U.K., 13-15 December 1993, Rapport technique de la NOAA NOSOES0006, 81 pp.
- Cheney, R., L. Miller, R. Agreen, N. Doyle, and J. Lillibridge, 1994: TOPEX/POSEIDON: The 2 cm solution. J. Geophys. Res., 99, 24,555-24,563.
- Minster, J.-F., C. Brossier, and P. Rogel, 1995: Variation of the mean sea level from TOPEX/POSEIDON data. J. Geophys. Res., 100, 25,153-25,161.
- Mitchum, G., 1994: Comparison of TOPEX sea surface heights and tide gauge sea levels. J. Geophys. Res., 99, 24,541-24,553.
- Nerem, S., 1995: Global mean sea level variations from TOPEX/POSEIDON altimeter data. Science, 268, 708-710.
- Rapp, R., Y. Yi, and Y. Wang, 1994: Mean sea surface and geoid gradient comparisons with TOPEX altimeter data. J. Geophys. Res., 99, 24, 657-24,667.
- Wyrtki, K., and G. Mitchum, 1990: Interannual differences of GEOSAT altimeter heights and sea level: The importance of a datum. J. Geophys. Res., 95, 2969-2975