A new extended Kalman filter has been developed. The initial aim is to assimilate altimeter data in a high-resolution non-linear model of the Tropical Pacific Ocean.
The innovative purpose of the filter is to represent temporal change of the error statistic in a low-dimension base, and to update the base over time to reflect dynamic changes in the assimilating model. An initial base for the assimilation process is defined from an EOF analysis of a sequence of representative state vectors.

Introduction

The ocean studies being conducted in the Pacific by ORSTOM, working with French teams (LODYC, LEGOS/GRGS) and American (NASA/GSFC, NOAA/PMEL), concern fundamental research into the ocean-atmosphere interaction mechanisms responsible for short-term climate variability in the tropics (from the seasonal signal to the interannual), and the effects of this variability on subtropical regions.
ENSO mechanisms and the dynamics of the warm pool, in connection with El Niño / La Niña, are core concerns.

ORSTOM has various economic de-velopment-related missions, and is therefore also involved with more applied research such as:

• helping to set up ocean observatories and operational forecasting centers,
• developing, distributing and follow-ing up forecasting products that will contribute to economic development in the Pacific region.

Against this background, the present study aims to set up a system for modeling, assimilating and using all available observations, in particular satellite data. The aim is to help provide the overview of theoretical and observational information of the ocean system best able to meet the research goals mentioned above. Below we outline a preliminary study for assimilating altimeter data into a primitive equation model, based on an original implementation of Kalman filtering: the SEEK filter.

SEEK filter

SEEK is a sequential assimilation method put forward by Pham et al. (1996). It is based essentially on extended (non-linear) Kalman filtering in which the equation for forecasting error trend is generated in a low-dimension space. A new statistically-relevant base is built to faithfully represent the definition and spatio-temporal change in this low-dimension base, but the other component elements of the filter are those of the conventional extended Kalman filter.

The reduced space is initially defined from an Empirical Orthogonal Function (EOF) analysis of a temporal state vector sequence. This reduced space (or base) changes over time during assimilation. Naturally, this makes the prediction error, and thus the propagation of observation-related information, dependent on real-time change in the system state vector and model dynamics. The change means that the definition of the initial base is not of crucial importance providing it is of a high enough rank. In practice, a few dozen to a hundred EOFs may initially be needed, although full Kalman filtering theoretically requires the complete dimension of the state vector, typically 10⁶.
The cost reduction is therefore enormous, and makes the problem applicable in realistic high-resolution cases, which is not true of the complete Kalman filter.
Multivariate fixed-base EOF projection has already been tested for linear cases in the tropical ocean (Cane and al., 1996). The main originality of the method described here is its general application to non-linear cases and, of even greater interest, the scope for changing the prediction error refer-ence base, which fully defines the properties of information propagation, i.e. error correction by the observations. Note also that the change in the base derives naturally from the Kalman equations, and does not involve an extra assumption; on the contrary it fits the filter's usual structure.
SEEK was first tested successfully with a quasi-geostrophic model in a very non-linear situation, capturing the turbulent interaction of mesoscale eddies at mid-latitudes in a closed domain (Pham et al., 1995).

Application to the tropical Pacific

The SEEK method was implemented in the Gent and Cane (1989) primitive-equation model, sigma vertical coordinate, enhanced by the NASA/GSFC team, in this part of the tropical Pacific.

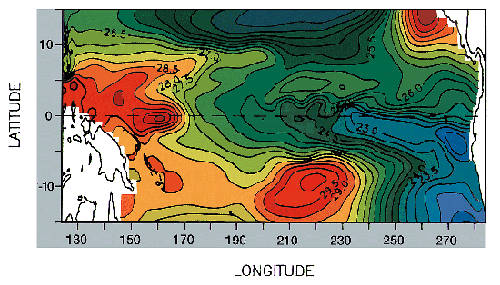
The "free" version of the model, i.e. forced by winds and the thermody-namics but not constrained by the observations, gives good results relative to what we know of the Pacific from observations (figure 1).

The advantage of the Gent and Cane model is its relatively modest computational burden, as it runs satisfactorily on the Nouméa Sparc20 workstation despite the state vector dimensions (greater than 400,000). The difference is not due to the nature of the equations, which are essentially the same as in other models, but to the reduced gravity assumption which reduces the active layer of the ocean to just a few hundred metres.
Deep ocean and topography effects, for example, are ignored.
This is obviously very much an approximation. But we have also known for a long time that it is reasonable to approximate the tropical ocean as two layers: recent results using the Gent and Crane model (Murtugudde et al., 1996) are convincing in this respect, and seem to show in partic-ular very realistic changes in the warm pool.

The SEEK assimilation scheme was thus implemented in the Gent and Crane (1989) primitive equation model. At this stage of our study, the model is forced by FSU monthly-averaged winds. A Kraus-Turner parameterisation is used for the upper mixing layer. Initial applications were begun on the scale of the entire tropical Pacific basin between 120°E and 8°0W, within latitudes ± 20°. In fact, the area extends between ± 30° latitude, but with a buffer zone between 20° and 3°0. The base resolution was 0.3° latitude by 1° longitude, over nine vertical levels.

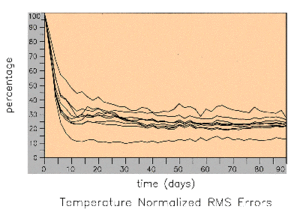
Today the approach can be consid-ered basically feasible, although some tuning is needed to better understand some of the filter properties. The results from twin control experiments are excellent, especially those concerning the vertical control of subsurface temperature fields. For simulated data with full physical consistency between the data and the model, surface altimeter data, as sampled by TOPEX/POSEIDON, provide very good control of the thermal structure in all the ocean layers processed, i.e. around 500 m. Figure 2 shows, for example, the error convergence (as a percentage) in the nine layers of the model from an initial random state by comparison with the reference experiment. After 20 days of assimilation, i.e. two TOPEX/POSEIDON cycles, the error on the global temperature fields decreases to below 5% of the initial error, across all layers in the model.
Initial experiments were conducted over the first three months of the TOPEX/POSEIDON mission, between October and December 1992.
The initial validations were positive but need refining as to the behavior of the filter's statistical properties and validation using independent data.
It is now important to extend this initial work to longer periods of time for which real validation with in situ observations will be more significant. Figure 3 shows a preliminary result, the surface temperature field, at the end of December 1992 after three months of assimilation of TOPEX/ POSEIDON data.