The Grenoble Group has developed a nowcasting/forecasting ocean model model of the Atlantic basin between 20 N and 60 N based on the (high) numerical resolution of the quasi-geostrophic equations. Forecast experiments were conducted during the period October 1992 to September 1993 to examine the predictability of the mesoscale flow field in the North Atlantic ocean. The predicted Gulf Stream is compared with the best estimate (or nowcast) obtained from the assimilation of TOPEX/POSEIDON (T/P) altimeter data in the model.

Gulf Stream nowcasting

The North Atlantic circulation was simulated using a high-resolution, QG model combined with the assimilation of altimeter data (e.g., Verron and Holland, 1989; Holland, 1989; Blayo et al., 1994). The numerical model is an extension of the two-layer quasi-geostrophic model by Holland (1978). In the present configuration, the ocean is represented by four layers, with three layers above the main thermocline and one layer below. The density within each layer is determined in accordance with in situ data fields. The first, second and third internal radii of deformation correspond to 30, 12 and 9 kilometres respectively. The horizontal grid mesh is 1/6 in both latitude and longitude, i.e. a constant grid step of 18.5 km in latitude and a variable grid step in longitude decreasing from 17.5 km at 20° N to 9.5 km at 60° N.

Recently, the four-dimensional behaviour of the ocean from October 1992 to September 1993 was reconstructed through assimilation of T/P altimeter data. The configuration and parameters of the assimilation scheme are fully described in Blayo et al. (1994). The assimilation procedure is a simple, sequential, along-track, nudging technique: the model surface streamfunction is controlled by observed quantities using a classical Newtonian relaxation term proportional to the difference between the model and observed sea surface heights. The coefficient of proportionality, which determines the strength of the observational constraints, is prescribed on the basis of previous experiments by Verron (1992).

The data used for assimilation in the control run consist of the T/P from 3 October 1992 to 26 September 1993 (cycles 2 to 37). The along-track sea-surface height (SSH), as provided in the GDRs, is directly assimilated in the model since it is linked to the model surface streamfunction observation because of inaccuracies in the geoid corrections. Therefore the total SSH is derived from the sum of the residuals and the surface height of the model averaged over the whole period of integration. T o adjust the mean SSH of the model, an iterative procedure equivalent to eight years of repeated annual simulations is applied.

In the Gulf Stream area, the mean circulation (the instantaneous model circulation averaged over one year of nowcasting) agrees fairly well with observations collected for years in the true ocean (Blayo, 1994; Blayo et al., 1994). Several properties of the North Atlantic circulation are particularly well reproduced, such as the path, penetration and recirculation of the Gulf Stream. The separation of the flow from the U.S. coast near Cape Hatteras is noticeably well simulated, as well as the robustness of the Gulf Stream to propagate to the north-western part of the basin (cf figure 1 A).

Estimates of the error budget in the T/P altimeter data are reported by Fu et al. (1994), leading to a general agreement of 5 cm for the total measurement of the sea-surface height. RMS is calculated a posteriori from the nowcast are consistent with this figure, decreasing from 7 cm in October 1992 to 6 cm in September 1993 (Brasseur et al., 1995).

Gulf Stream forecasting

The same model operated without assimilation (forecast experiments) is significantly different from the run controlled by assimilation (nowcast simulation). It was thus important to assess the extent to which the streamfunction in the nowcasting mode can be considered the best estimate of the true ocean, in much the same way as meteorologists consider daily analyses of the atmosphere to be representative of the reality.

Using the nowcast as a reference, auxiliary experiments were conducted to address three questions:

• How does the model with assimilation differ from a so-called "pure forecast" trajectory, as produced without altimeter data?
• Can the model controlled with T/P altimetric residuals be considered a good description of the actual ocean trend?
• Is the assimilation useful for predicting the future of the system, in the short and medium terms?

These questions are examined in Brasseur et al. (1995), using twin experiments obtained from the assimilation of subsets of the original T/P data set (covering, for instance, only part of the total duration for the reference experiment), or from the assimilation of synthetic altimeter data extracted from the reference simulation.

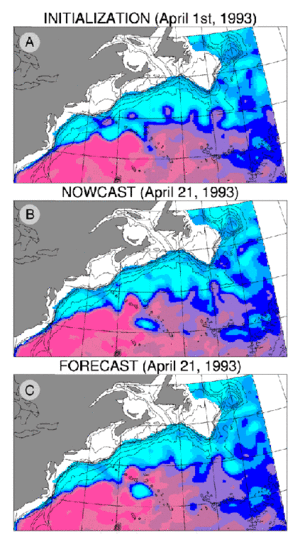
On the basis of the assimilated run, a predictability experiment was also conducted to estimate the doubling time of small errors in the initial conditions, to derive predictability time scales, and to evaluate how far from ideal the model is. The predictability experiment consists of 20 forecast experiments initialised with 20 slightly different ocean states: the initial conditions are taken as snapshots of the nowcast simulation at three-day intervals, and integrated over time in a forecasting mode. Figure 1 illustrates one of these experiments. The duration of the predictability experiment, 60 days, should avoid the bias introduced when looking at a single trajectory, which could derive from an initial condition representative of a particularly stable or unstable conformation of the flow.

Predictability and model assessment

Predictability statistics were computed according to the methodology suggested by Lorenz (1982) to study the predictability of atmospheric flows. Our estimated doubling times are of the order of 18 days in the North Atlantic basin. Other authors (e.g. Adamec 1989) found values close to 13 days in simulations resolved by three modes; however, they were looking at an idealised Gulf Stream system over a flat bottom, which is probably more unstable than the flow over the North Atlantic basin. The corresponding figure for the atmosphere is 2.5 days according to estimates reported by Lorenz (1982).

The predictions of the mesoscale flow field at a two-month range are found to be totally decorrelated from the true ocean, i.e. bounded by the predictability time scales. These bounds are largely inherent to the physical nature of the system and the associated equations.