The wave fields from the VAGATLA model are corrected by Optimal Interpolation of the altimeter Significant Wave Heights (SWH s). Internal calibration of the method shows the TOPEX SWH s are unbiased. The results are compared with buoy measurements. They confirm the quality of wave heights measured by buoys, and the contribution altimeter data can make to correct SWH values in the model.

Introduction

The simplest way of enhancing wave fields produced by models is to merge altimeter data with model outputs using an optimal interpolation scheme. The scheme is applied to the difference between the observation and the model. The observation used is the mean, on a model grid, of the SWH s derived from TOPEX waveforms. The model data are SWH values at the corresponding points in the field output by Météo-France's VAGATLA model.

Optimal interpolation theory for a wave field

Each model output is at the centre of a six-hour temporal window, during which altimeter observations are made at grid positions called observation points. The correction needed at each point in the grid (each calculation point) is a linear combination of the differences between the measurement and the model at the different observation points. The coefficients of the linear combination are chosen to the mean square error of the result (value analysed). They are then taken as the solution of the system. The term where line i crosses column j in the matrix is the mean product of the differences for grid points i and j. The second term contains, for line i, the mean product of the differences at grid point i and the model error at the calculation point.

The accuracy of the results depends on the assumptions made in calculating these two terms. Using times at which points i and j are observed simultaneously, it is possible to calculate, almost exactly, a matrix for the linear system from the data. But the second term needs an estimate of the model (or altimeter) bias and standard deviation.

Let us model the altimeter error, with the means at constant true wave heights:

bias : <eobs> = -aobs(<SWH > - Hcentre) (1) variance : <(eobs - <eobs>)²> = -b <SWH >² (2)

We can then resolve the system, whose unknowns are the bias and standard deviation. The first equation assumes that SWH bias is zero for SWH = Hcentre, the value being initially close to the mean value (2 m) and the altimeter tends to approach that value (aobs>0). The second equation assumes that the mean square error is proportional to the value observed. Both equations use the results of comparisons between different altimeters, buoys and models; some of these results have appeared in the literature.

Calibrating the method, results

Calibrating the scheme consists mainly in setting coefficients Hcentre, aobs and b relative to the error fields. This was done in TOPEX cycle 1, using a positive loop induced by (1) and (2), which alters the coefficients until the fields no longer have negative waves. We therefore obtained aobs=0, which shows, independently of any measurements, that the TOPEX altimeter supplies unbiased SWH s.

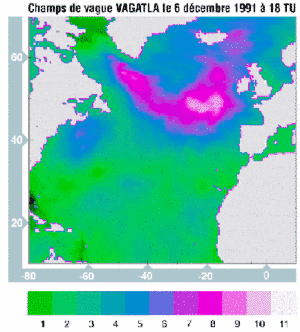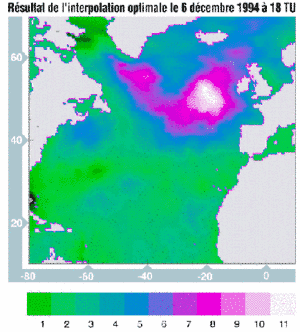Figure 1 : VAGATLA wave field (in m) on December 6, 1994 at 18:00 UTC	Figure 2 : Wave field (in m), result of optimal interpolation on December 6, 1994 at 18:00 UTC.

Figures 1 and 2 show a situation in which the measurements raise the wave field by more than 3 m. In other situations, VAGATLA overestimates wave heights, and the altimeter can reduce the SWH model outputs by more than 4 m.

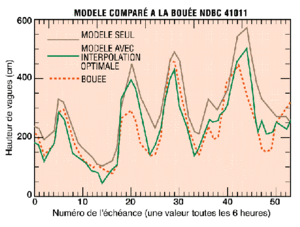
Figure 3 shows a model/buoy comparison, with and without altimeter data. On average, the altimeter data using optimal interpolation bring the model estimate closer to that of the buoys.
The improvement is 30% (10 cm) in bias and 7% (7 cm) in standard deviation. Naturally, when the altimeter data are in the immediate vicinity of the buoy they make a particularly significant contribution to improving the model estimate. See, for example, instants 27 and 48 in Figure 3.

Conclusion

Altimeter SWH s considerably improve wave model outputs. The next stage will be to spread the changes in wave energy over the components of the sea-state spectrum and, while running the model, use the contribution obtained at given instants.