TOPEX/POSEIDON has provided the first opportunity to test global ocean general circulation models in a wide range of spatial and temporal scales. Comparisons of the observations are made to simulations by a state-of-the-art model driven by realistic winds, with very encouraging results on the mesoscale variability, the annual cycle, as well as intraseasonal and interannual changes.

TOPEX/POSEIDON (hereafter T/P) is the first altimetric satellite specifically designed for studying the global ocean circulation. The unprecedented measurement accuracy and continuous global coverage has made the data an excellent testbed for global ocean general circulation models. In this study we use the first two years of the T/P data for comparison to simulations, for the same period, by the model developed by the Parallel Ocean Program (POP) at Los Alamos National Laboratory (Smith et al., 1992).

The POP model employs a Mercator grid that covers the global ocean from 78° S to 78° N with 1280 grid points in longitude, 896 points in latitude, and 20 vertical levels. The horizontal resolution varies from 31.25 km at the Equator to 6.5 km at the highest latitudes, the average over surface ocean points being 22.2 km or 1/5 . With more than 11 million ocean cells in the three-dimensional grid (50 times larger than the 1/2 model), these are the finest resolution global simulations performed to date.

After spinning up the model from rest for about 30 years, a 10-year simulation was performed using the POP model. While this is a relatively short integration time compared to the 1000+ years needed for the density field of the deep ocean to reach equilibrium, it is long enough for the upper ocean to have reached a quasi-equilibrium: the geostrophic adjustment of the velocities to the density field is for the most part completed. The simulation was driven by surface wind stress fields derived from the twice-daily analyses from the European Centre for Medium-Range Weather Forecast (ECMWF) and averaged over 3-day intervals for the period 1985-1995. The surface heat flux was parameterized by the difference between the sea surface temperature and climatology based on the analysis of Barnier et al. (1995). The surface salinity field was nudged to the Levitus seasonal climatology with a relaxation time scale of 30 days.

Mesoscale Variability

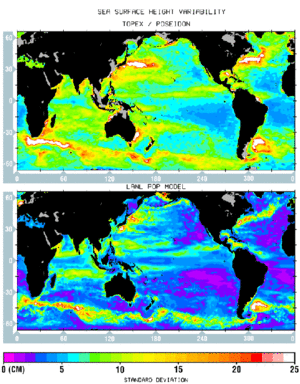
Figure 1 shows the standard deviations of the residual sea surface height after the two- year mean is subtracted. The model simulates the distribution of the variabilities fairly well, having reproduced the zero-order features of the observation, namely the concentration of eddy energy in regions of strong currents (e.g., the Gulf Stream, the Kuroshio Current, and the Antarctic Circumpolar Current, ACC). However, the model fails to produce the extension in the Kuroshio and Gulf Stream currents, which separate from the coast too far to the north, a long-standing problem with ocean circulation models. These and other errors in the mean circulation are likely due to deficiencies in the model density distribution associated with a combination of errors in the initial conditions, the subgrid-scale mixing parameterizations, the heat and freshwater forcing, and possibly inadequate grid resolution. Secondary maxima in the tropical oceans are well reproduced, but the maxima observed along 20° -25° latitude in both the western North Pacific and western South Pacific as well as the maximum between Africa and Madagascar are missing from the model simulation.

The global mean standard deviation is 8.9 cm for the observation and 5.1 cm for the simulation. In regions of weak variability, the difference may be ascribed to observational errors which are comparable to the measurements. In the eastern South Pacific the minimum variability is 4.1 cm for the observation and 1.3 cm for the simulation. Assuming the model represents the true level of variability, the observational error would then be (4.12 - 1.32 )½ = 3.9 cm, which is actually somewhat less than the combination of the estimated measurement and tidal errors, (3 2+ 4 2 )½ =5 cm. However, in regions of strong variability the observational error is too small to account for the discrepancy: if we take 3.9 cm as the global observational error, then the true global mean variability should be (8.92 - 3.92 )½ = 8 cm, still about 3 cm higher than the simulation. We conclude that the model variability is too weak, especially in the eddy-active regions.

The Annual Cycle

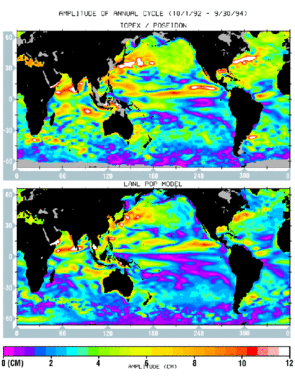
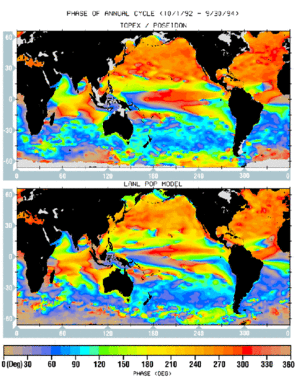
Figures 2 and 3 show the geographical distribution of the estimated amplitude and phase of the annual cycle. To extract the annual signal, a least-squares fit of an annual harmonic was made to the sea level time series at each point. The amplitudes of the resulting sine and cosine terms were smoothed over an elliptical area of 600 km (zonal) by 300 km (meridional) to average out the mesoscale energies while maintaining the finer zonal structures. Since only two years of data were analyzed, the statistical uncertainties are high in regions of large interannual variability such as the tropical Pacific.

Overall, the agreement between the patterns of both amplitude and phase is excellent. The model simulation has a generally weaker amplitude than the data which may point to deficiencies in the treatments of surface heat fluxes and vertical mixing in the upper ocean.

The highs in late summer/early fall and the lows in late winter/early spring are the prevalent features in both hemispheres from 20° to 45° latitude. The northern hemisphere has a stronger annual cycle than the southern hemisphere (Cheney et al., 1994), because it contains more land, which creates stronger air-sea heat exchange, especially over the western part of the ocean.

The high-latitude (> 45° ) southern hemisphere has a weak annual cycle with a six month phase difference from that at the mid-latitudes. The T/P observations are the first to show this extremely low annual variability along the path of the ACC. The variability of the ACC transport in the model, which is primarily controlled by the wind forcing, also exhibits no pronounced annual cycle.

At low latitudes (20° S - 20° N), for instance in the Arabian sea, there are two regions of high annual amplitude with opposite phases. The one east of Somalia is the so-called great whirl formed in June, and the one near the southern tip of India is formed in January (Bruce et al., 1994). These are the ocean's response during the two opposite phases of the annual monsoon wind cycle.

The annual cycles in the tropical Pacific and Atlantic are primarily associated with annual variations of the North Equatorial Counter Current which flows eastward against the Trade Winds. In the Pacific the annual cycle has two maxima: one along 12° N from 220° E to 270° E, and the other along 7° N from 180° E to 250° E (Perigaud, 1990), which both show westward phase propagation. The model apparently fails to simulate the proper magnitude for the maximum along 7 N. In the eastern South Pacific and South Atlantic, the annual cycles are associated with coastal upwelling systems off the west coasts of South America and Africa between 0° and 30° S. The sea level starts to rise near the coast in January followed by a rise in offshore regions in the ensuing months. For both the simulation and observation, the upwelling systems extend northwest towards the equator and are bordered to the west by a line of minimum variability (a band of magenta in the amplitude maps).

Intraseasonal Variability

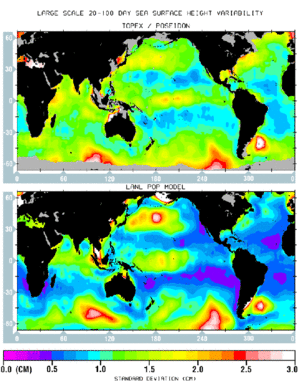
Figure 4 shows the geographical distribution of the large-scale intraseasonal variability, i.e. the standard deviations of the surface height averaged over 10° x 10° boxes and band-pass filtered to retain energies at periods from 20-100 days and length scales larger than 1000 km. This removes the mesoscale variability

The ubiquitous mesoscale eddies make satellite observations a more viable approach to studying large scale variability than using in-situ measurements, especially at intraseasonal time scales: the T/P observations are the first to reveal large-scale eddy structures and geographical distributions. Significant energy is contained in oscillations which are coherent over thousands of kilometers. Although the standard deviations are a few cm, peak-to-peak changes can reach 20 cm over areas of thousands of km in the Southern Ocean.

The model simulation is in good agreement with the observation, especially in the Southern Ocean where the intraseasonal energy is highest. In the model these fluctuations are highly correlated with the depth-integrated transport streamfunction, indicating that the associated motions are depth-independent (barotropic).

Furthermore, oscillations with periods less than 60 - 70 days disappear if monthly-mean rather than 3-day winds are used, indicating that this is a barotropic response of the entire water column to the high-frequency wind forcing.

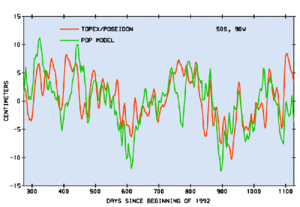
This conclusion is confirmed by recent more detailed analysis of the T/P data (Fu and Davidson, 1995). In the southeastern Pacific (see Figure 5), the agreement is excellent, indicating that the wind product from ECMWF is quite good. This is somewhat surprising since few wind observations are available in the southern hemisphere.

Interannual Variability

Figure 6 shows the difference between the 1994 and 1993 April monthly-mean surface heights. The character of seasonal changes in both the atmosphere and ocean is different every year. These interannual changes are the primary focus of the climate problem.

A major feature is a large sea level increase in the western tropical Pacific and a corresponding decrease in the eastern Pacific caused by the stronger westward trade winds in 1994. The trade winds relaxed in June 1994 and triggered the 1994-95 warm episodes in the tropical Pacific (Liu et al., 1995). This feature and many others are simulated very well by the model. The overall correlation between the two maps is 0.64. Since there are no interannual changes in the climatological surface heat and freshwater forcing in the simulation, this good agreement must be solely attributed to the model response to realistic wind forcing. It remains to be seen to what extent the use of realistic heat fluxes would further improve the simulated interannual surface height variability.

Concluding Remarks

The results of the present study have demonstrated the complementarity between satellite observation and computer simulation for studying the global ocean circulation. The agreement between the two suggests that the model has incorporated the physics governing the wind-driven, adiabatic component of the circulation quite well, as evidenced by the success of the simulation of the intraseasonal variabilities as well as the variabilities of the tropical ocean in general. The discrepancies on the other hand reveal the places where the dynamics and thermodynamics of the model need improvement, primarily in the mid- and high-latitude regions. The satellite observations provide the first test of the model on a truly global scale. Conversely, many aspects of the satellite observations would be difficult to interpret without a realistic model. Ultimately it will be necessary to assimilate the data into a model to obtain an optimal estimate of the full three-dimensional state of the ocean. The methodologies for doing so involve techniques from estimation and control theories, but these pose formidable difficulties due to the large number of variables in an ocean model (approaching 108 in the present case). However, potentially effective optimization methods are currently under development (Fukumori and Malanotte- Rizzoli, 1995).

Acknowledgments

Computer programming and graphics assistance provided by Greg Pihos is gratefully acknowledged. Part of the research described in the paper was carried out by the Jet Propulsion Laboratory, California Institute of Technology, under contract with National Aeronautics and Space Administration. Support from the TOPEX/POSEIDON Project funded under the NASA TOPEX/POSEIDON Announcement of Opportunity is acknowledged (LLF). The POP model development and simulations were funded by the DOE CHAMMP program, and computing resources were provided by the Advanced Computing Laboratory at Los Alamos National Laboratory.

References

• Barnier, B., L. Siefridt, P. Marchesiello, J. Marine Systems, 6, 363-380 (1995).
• Bruce, J.G., D. R. Johnson, J.C. Kindle, J. Geophy. Res., 99, 7651-7664 (1994).
• Cheney, R. E. et al., J. Geophy. Res., 99, 24555-24563 (1994).
• Fu, L.-L. and R. A. Davidson, J. Geophys. Res., 100, in press (1995).
• Fukumori, I. and P. Malanotte-Rizzoli, J. Geophys. Res., 100, 6777-6793 (1995).
• Liu, W.T., W. Tang, and L-L. Fu, Eos, Trans. Amer. Geophys. Union, Vol. 76, No. 43, p.429, 437 (1995).
• Perigaud, C., J. Geophy. Res., 95, 7239-7248 (1990).
• Smith, R. D., J. K. Dukowicz and R. C. Malone, Physica D, 60, 38-61 (1992)